---

---

Class Page

For

Larousse Charlot

---

THE PROBLEM: Let angle A of triangle ABC have measure 120 degrees.
Let A' be the point of intersection of segment BC and the angle
bisector of angle A.
Likewise B' is the intersection of AC and the angle bisector of angle
B, and C' is the intersection of AB and the angle bisector of angle C. Prove angle B'A'C' is always a right angle.

Solution:

Consider the triangles DCAA’ and DAA’B. We know that BB’ is the bisector of the angle ÐB. Similarly CC’ is the bisector of the angle ÐC. If we let AB be the bisector of an exterior angle the triangle ACA’, then C’ is the excenter of triangle ACA’. Hence, A’C’ is the bisector of ÐAA’B.

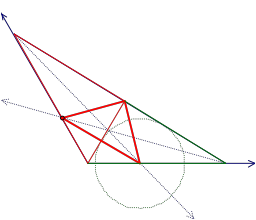
Similarly, let AC be the bisector of an exterior angle of triangle AA’B. Then, B’ is the excenter of triangle AA’B, and A’B’ is the bisector of angle ÐAA’C.

Take notice that the sum of angles ÐCA’A and ÐAA’B is 180. Also that ÐAA’C’= ÐC’A’B; similarly,

ÐCA’B’ = ÐB’A’A.

So, we then have the following

180 = ÐCA’B’ + ÐB’A’A + ÐAA’C’ + ÐC’A’B

= 2ÐB’A’A + 2ÐAA’C’

Multiply the equation by ½ and we obtain that

90 = ÐB’A’A + ÐAA’C’

which is right. Thus, the triangle DB’A’C’ is a right triangle.¨

Click here to see the triangle

---

Return

---